秋山仁特別賞
樹形に見る樹木の成長戦略
―アカメガシワ(Mallotus japonicus)を例として
![]()
上杉曉
- 東京都城北学園中学校 3年
上杉曉 -
第51回入賞作品
中学校の部
秋山仁特別賞
昨年度、私は『タケの美しさの秘密』と題する研究で、タケがフラクタルであることを示した。樹木はどうであろうか。アカメガシワを材料に、様々な部位を測定して樹形の特徴を導くとともに、樹形が「自己相似性」をもつ図形=フラクタル=であることを証明する。また樹形がタケと異なる点、さらには成長の仕方の違いについて、その理由と共に考察する。
《原理》
(1)フラクタル
ある形のどの部分を拡大、縮小しても元の形と同じくなる、すなわち「部分」と「全体」とが酷似するという性質を「自己相似性」という。この性質をもった図形を「フラクタル」と呼び、自然界の様々なものの形態に表れる。フラクタルの理論は1975年にフランスの数学者ブノワ・マンデルブロによって発表された。
(2)双子葉植物と単子葉植物の成長戦略
双子葉植物と単子葉植物とでは、成長する時の「形成層」の有無が大きく異なる点だ。種子植物には2つの成長がある。1つは伸びる方向の成長で「伸長成長」と呼ばれるもので、根や茎の先端にある頂端分裂組織によって行われる先端成長が主である。もう1つは、茎が太くなる「肥大成長」だ。肥大成長はさらに2つに分けられる。その1つが「一次肥大成長」だ。これは成長点で先に向かって伸びると同時に、茎も太くなる成長である。この一次肥大成長だけで終わらずさらに肥大成長を続ける植物もあり、その場合の肥大成長を「二次肥大成長」という。双子葉植物の場合は、茎の中で放射状に並んだ維管束の木部と師部の間をつなぐ輪のような分裂組織「形成層」を生じて、そこから内側へ木部を形成しながら太くなっていく成長である。この二次肥大成長によって、幹や枝は必要なだけ大きくなれる。幹を途中から失った場合でも、代わって枝が太くなって幹となり得る。しかし、タケなどの単子葉植物の多くは、維管束がまばらに並んだ構造をしていて、双子葉植物のような形成層がないので二次肥大成長を行わず、枝が幹になることはできない。
(3)成長曲線
生物の個体・器官の成長量もしくは群(集団)の成長量を経時的に測定し、横軸に時間、縦軸に成長量をとってグラフにした。典型的な成長曲線にS字状のシグモイド曲線、ゴンペルツ曲線がある。
《アカメガシワ》
研究材料は、被子植物門双子葉植物綱トウダイグサ目トウダイグサ科アカメガシワ属のアカメガシワ(Mallotus japonicus)だ。朝鮮半島や中国にも分布する落葉樹で、日本では秋田、宮城以南に分布する。和名は、新芽が赤く、カシワのように葉を食物を載せるのに用いたことに由来する。

《樹木の特徴》
(1)樹形
幹や枝、葉などを総じた樹木全体の形を「樹形」といい、「卵形」「傘形」「不整形」「株立ち」「伏生形」などがある。アカメガシワの場合、2冊の図鑑には「卵形」さらには「株立ち」とあったが、今回のものは「不整形」だった。このことは「樹形というものは、完璧に定まってはおらず、生育環境によって大いに変化し得る」ということを示している。
(2)樹高
10m以上を「高木」、10m以下から数mを「小高木」、数m以下を「低木」、1m以下を「小低木」という。アカメガシワは8~15mになる高木だ。(3)枝のつき方:幹から枝が出る時の角度が樹木の形を決める。針葉樹は枝が整然と生え、均整のとれた形をしている。広葉樹では規則性はあるが、針葉樹のように一定の法則性はない。広葉樹の枝の分かれ方には、2つに分かれる「二叉分岐」と3つに分かれる「三叉分岐」がある。アカメガシワには両方の分かれ方があるが、三叉分岐が主流と思われる。
アカメガシワの測定
近所の林に生えているアカメガシワを、所有者の許可を得て伐採し、各幹や各枝には判別を容易にするために記号をふった。
《記号の付け方》
分枝するごとに太い方からa、b、cと付ける。例えば一番太い幹aから分枝した横枝は太い順にaa(a2と略記)、ab、acとする。横枝a2から分枝した脇枝は太い順にa2a(a3)、a2b、a2cとする。
《測定》
樹木の全長、幹の太さ、横枝の間隔、横枝の長さと太さ、脇枝の間隔、横枝の太さ、脇枝の長さと太さなどを、それぞれ根元から順に測定した。
《結果と考察》
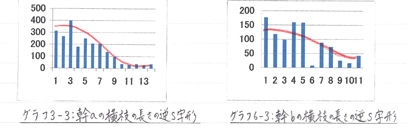
| (1) | 幹a、幹bにおいて横枝の間隔の積算値グラフは、ともに中央部がふくらんだ曲線となった。横枝の太さを横軸に単純に並べたグラフではa、bともに最初は緩やかで、途中から少し急になり、また緩やかになる「逆S字形」になった。積算値グラフもともに相似な曲線を描いた。横枝の長さの単純グラフもやはり逆S字形で、積算値グラフもともに中央部がふくらんだ曲線になった。このように幹a、bは横枝の間隔・太さ・長さの比率が類似しており、相似図形であると言える。 |
| (2) | 横枝(ab、a2b、a3ba2)の太さの単純グラフでは、a2b以外は逆S字形と言えなくもない。積算値グラフは中央部がふくらんだ曲線になった。横枝(ab、a2b、a3ba2)それぞれの脇枝の間隔では、ab、a2bの積算値グラフがS字状にふくらんだ曲線を作った。脇枝の太さの単純グラフでは、逆S字形になっているのはa3ba2だけだったが、積算値グラフは平たいS字状になった。脇枝の長さの単純グラフでは類似性は見られないが、積算値グラフではふくらんだ曲線になった。脇枝の葉の枚数についても単純グラフでは、横枝abとa3ba2では逆S字形、積算値グラフでは平たいS字状になった。以上のことから、横枝のグラフには基本形のようなものは認められるが、いたるところで差異がみられ、完全な相似形ではないと考えられる。
|
| (3) | 枝の間隔や太さ、葉の枚数を単純に並べたグラフは逆S字形である。積算値グラフはS字状となる傾向がみられるので「自己相似性をもっている」と言える。これは即ち、樹木の樹形はおおむねフラクタルだということだ。 |
| (4) | 樹形図を描くと樹木全体や幹、横枝の多くが逆三角形をしており、同じ図形が連なっていることはフラクタルであることを示している。 |
フラクタルのゆがみ-アカメガシワの成長戦略
①成長とフラクタル
樹木の形がフラクタルになるのは、各部の成長の仕方が共通しているからだ。遺伝子か何かによって、一定に決められているのではないか。
②環境と成長戦略
樹木のすべての部位がフラクタルだと、日当たりの問題が起きる。それを解決するために樹木は枝や葉の位置や長さ、太さ、あるいは余分な部分を枯らすなどして、形を変えるのだ。
②幹になり得る枝
幹になるか枝になるかは、環境による太さの変化にしか過ぎない。三叉分岐では、日当たりなどの環境の悪い1本が弱ったり枯れたりしている。樹木は2本の枝が育つように、あらかじめ3本の枝を出して「保険」をかけているのではないか
タケとの比較-双子葉植物の戦略
 ①アカメガシワのS字曲線はあまりはっきりしないが、タケと同じシグモイド曲線を形成して成長する。
①アカメガシワのS字曲線はあまりはっきりしないが、タケと同じシグモイド曲線を形成して成長する。
②成長戦略の違い:タケのような単子葉植物は二次肥大成長ができない。そのため幹は他の枝とは完全な区別があり、真っすぐ伸びる。単子葉植物は元々が環境の悪い地域に進出した植物だからだ。アカメガシワのような双子葉植物は、栄養分の多い土壌に生育した。そのため樹高は高くなり、大規模な森林を形成した。枝が幹になる能力も、3本の枝を出して「保険」をかける知恵も、鬱蒼とした木々の中で日光を得る手助けになったのに違いない。
《結論》
アカメガシワの樹形は自己相似性をもつフラクタルだ。測定値の積算値グラフはシグモイド曲線だった。しかしそのフラクタルにはゆがみが多く、これは環境に適応する成長戦略の差異であった。双子葉植物の方が単子葉植物よりも環境に適応して大いに変容する。「植物はフラクタルであるが、環境や分類によってはその形を大いに変え得る」ということだ。
審査評[審査員] 秋山 仁
自然界にある動植物の形状、形態、成長法に潜む謎を数学的な視点に立ち、考察した読みごたえのある作品である。上杉君は昨年(2009年)、「竹の美しさの秘密―数学的に見た竹の形態」と題した研究を夏休みの自由研究として行っている。今回は、その研究の継続とも言える。
竹とアカメガシワの本質的な違い、即ち、前者が単子葉植物であるのに対し、後者が双子葉植物であることに注目して研究を進めている。
双方の共通点として、どちらも形態がフラクタル(自己相似)になっていることや、成長の際にどちらもシグモイド曲線を形成していることなどを実際の木から計量的に検証している。
特に興味深いことは、これら2つの植物の成長戦略には大きな違いがある原因を、以下のように突き止めていることである。
単子葉植物は、2次肥大成長を行えないのに対し、双子葉植物はそれができるので、枝が幹に、また、都合の良い幹や枝を発達させることが可能だから。
以上の研究は植物学的にも大変立派であり、秋山仁特別賞に適わしい。
高校生になっても、自然の中に潜む神秘に科学的にメスを入れ、新しい発見を次々に成し遂げていただきたい。























指導について上杉富之
本研究は、本人が関心を持っている生き物の形(形態)に焦点を当て、「生き物の世界を丸ごとつかみ取る」ことをテーマにして行った研究です。具体的には、家の近くに生えていたごく普通の雑木(アカメガシワ)を1本丸ごと切り倒し、その木の幹や枝・小枝の太さや長さ、葉の枚数などをまさしく枝葉末節に至るまで測定するというきわめて「原始的」な研究でした。炎天下やヤブ蚊に刺されながらの測定に研究を中断し、また、大量の測定結果を前にしてのデータの集計や考察に音をあげかけたこともありました。が、最終的には、1本の木としてのアカメガシワの形態を丸ごと測定・分析し、その結果を基にして植物全体の成長戦略にまで考察を広げることができ、本人なりに当初の目的を達成できたのではないかと思います。
今回の受賞は、常日頃より理科学習をご指導いただいている先生方のおかげだと感謝しております。