秋山仁特別賞
私はどこにしようかナ?
~人間ピラミッドにおける位置と重さの関係に関する考察~
![]()
河合 千晶
- 三重県鈴鹿市立河曲小学校 5年
河合 千晶 -
第46回入賞作品
小学校の部
秋山仁特別賞
6月から運動会の組体操の練習が始まった。3段から始め、4段に挑戦。ここで問題が発生した。「だれが一番下の列をするか、どこが一番楽か……」。担当する場所を決めたり、くずれにくくするための法則や性質はないだろうか。人間ピラミッドを成功させるためにも、科学的な視点で、安全に、だれもが安心して、その上、かっこよく築くための研究に取り組みたい。
5段ピラミッドでは、4段目までに1+2+3+4=10人が乗っている。一番下の5人で10人分を支えるから、10÷5=2……。一番下の段の1人は2人分を支えればよいと、学校ではみんなが考えている。その一方では経験的に、端の方が楽だとも知っている。そこで、次のことを中心に調べる。
・モデルを使い、人間ピラミッドのそれぞれの場所の支える重さを調べる。
・安全な仕方を科学的に考える。
〈1〉人間ピラミッドの場所と支える重さの関係
〈方法〉
厚紙とひごで作った人間ピラミッドの人モデルを36個用意する。単行本をおもりに、さらに紙をはさんで、それぞれの人モデルの重さが200gになるように調整する。それをピラミッドに組み上げ、各段それぞれの人モデルにかかる重さを上皿はかりで量る。

〈予想〉
3段のピラミッドで、一番上の人が乗る前の下2段の状態を考えてみる。一番下の段(3人)の端の人の背中には、上の段(2人)のうちの1人の片手、片足が乗っている。一番下の段の真ん中の人には、上2人の片手、片足が乗っている。
| 一番下の段の端 | =(片手・片足) =0.5人分の体重 |
×1人 |
| 一番下の段の真ん中 | =(片手・片足) =1人分の体重 |
×2人 |
このように、一番下の段の真ん中の人は大変(不公平)だと予想できる。
さらに一番上に1人乗るから、等しく支えるとして、1人÷3=0.33……人分が一番下の3人それぞれに加わるだろう。結局、一番下の段の端の人には0.8人分、真ん中の人には1.3人分の体重がかかるはず。
〈結果〉
( )の数字は何人分か計算した値
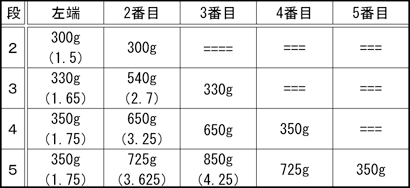
〈考察〉
3段目の予想と実験の結果がずれた。予想では自分(人モデル自体)の重さ(1人分)を加えて、端の人の重さは1.8人分、真ん中の人は2.3人分としたが、実験結果はそれぞれ1.65人分、2.7人分だった。最後に一番上に1人が乗ったときの分担重量を1人÷3=0.3人分と考えたことに問題があった。
そこで次のように、3段目の人の式を考えた。
端=0.5+(一番上の分担)+(自分)
真ん中= 1+(一番上の分担)+(自分)
この式に、自分=1、端=1.65(実験結果)、真ん中=2.7(実験結果)を当てはめると、一番上に乗る人の体重が3段目の人にどう分けられるか(一番上の分担)が計算できる。
端にかかる分担=0.15人分
真ん中にかかる分担=0.7人分
このように、頂上に乗る1人分は、公平に÷3ではなく、場所によって違う分担の仕方をする。
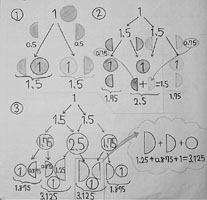
そこで次のような計算〈千晶理論(2)〉を考えてみた。
〈千晶理論(3)〉どの段でも端の人は2人分を超えることはない。つまり、増えるけれど限りがある。 端の人の増え方は少ない。
千晶理論(2)の
〈公式〉ある段の端=一つ上の段の端÷2+1
を使って、
2段目の端=1÷2+1=1.5
3段目の端=1.5÷2+1=1.75
4段目の端=1.75÷2+1=1.875
5段目の端=1.875÷2+1=1.9375
と計算できる。ここである段で2よりわずかに小さいとき、その下の段の端も2を超えない。
| 次の端 | =2よりわずかに小さい数÷2+1 | (あ) |
| =1よりわずかに小さい数 2+1 | (い) | |
| =2よりわずかに小さい数 2+1 | (う) |
(あ)(う)の両方に「2よりわずかに小さい数」とあるが、計算をみると(あ)より(う)の方が2に近い。 つまり、公式をくり返し使うと、段が増えるにつれて数は大きくなっていくが、2を超えない。
千晶理論(2)でも、まだ実験結果とわずかなずれがある。ピラミッドが高くなるにつれて、「たわむ」ことが関係しているのかもしれない。
〈2〉アーチ橋で空中に浮いた石の重さの配分(略)
千晶理論(1)
なお、上皿はかりの計量では、単行本の向きや重さ調整ではさんだ紙の位置によって、目盛が左右対称にならないことがあった。逆に左右対称のときはピラミッドはじょうぶだった。こうして、安全に、安心してピラミッドを組み上げるための理論ができた。
〈千晶理論(1)〉バランスの良さは、高く組み上げるための大切な条件である。右手と左手、右足と左足にはできるだけ平等に力をかける必要がある。
研究の反省と感想
算数を使って、人間ピラミッドの大変さを数値で表した。体がかたいこと、全員の体重が等しいことなど、理想的な状態で考えた。計算の結果、祖父の時代にいわれたような根性論だけでは、人間ピラミッドを完成させることはできないのは確かである。
審査評[審査員] 秋山 仁
運動会での人気競技である人間ピラミッドにおいて、どの位置が大変で、どの位置が楽かを数理的に考察しようという、いかにも小学生らしい興味に端を発したテーマである。ピラミッドが5段の場合、一番下の5人で上に乗る10人を支えるのだから、下の5人のどの人も10を5で割って、2人分を支える、と考えるのは正しくない。そこで、彼女は数多くの実験を行い、以下に示すいくつかの真実に辿りついている。
| ① | 高く積み上げるには、左右の手、足に平等に力をかけること |
| ② | ピラミッドの各位置にかかる力を求める公式を独力で導出していること |
| ③ | どの段でも端の人は2人分を超えないこと |
| ④ | 予想通り、一番下の中央の人に一番多くの負担がかかり、n段のピラミッドの場合、約n人分の力がかかること |
などである。
この作品を読んで、筆者はパスカルの三角形の変種を想起した。本作品で彼女が考えたことは、高校数学を用いれば、より一般化でき、式(漸化式)で表現できそうだ。是非、高校に入ったら試してみていただきたい。






















指導について鈴鹿市立河曲小学校 三浦靖樹
1学期の終業式の日、「ピラミッドを指導する上できをつけていることは何ですか」と質問を受け、①土台となる1段目に、身体が大きく、力も強い子を配置する。②1.2.3の各段は、背中がフラットになるように気をつける。③5段目は下に負担をかけずに素早く乗れる子を選ぶ。と答えました。研究の結果、各段の真ん中に一番荷重がかかるということがわかり、実際の指導にも大変役立ちました。
自分がこれからチャレンジすることを研究材料とし、科学的に分析して、成功に結びつけようとする千晶さんの気持ちに対して感心するとともに、「科学者魂」をみる思いがしました。
9月の運動会で5段ピラミッドが全て成功できたのは、この研究による「科学的な根拠」とみんなの気持ちが一つになったからに間違いありません。