ボウリング場でストライクがとれなく困っていた時、出会った“ストライク名人”のおじさんから「右利きの場合、１ピンと３ピンの間にストライクが取りやすい“ポケット”がある」と教えられた。真正面の１ピンではなく、なぜ１ピンと３ピンの間なのか、なぜストライクが出やすくなるのか。僕もたくさんのストライクを取れるようになりたいと、研究を始めた。

《１》ストライクが出る「ポケット」はどこ？

【実験装置】

　家にあったおもちゃのボウリングセットを利用した。ピンはちょうど実物の1/2の大きさなので、ピンの配置なども1/2に調整した。ボールは傾斜レールで転がして当てる。角度は５ピンを基点に１ピンと結んだ線を０°とした。

【実験①】

ポケットの角度を探す。

《方法》

１ピンと３ピンの角度は、基点の５ピンから０°と30°。そのため右０°～30°の範囲でストライクの出た角度を調べる。ボールは１°ごとに10回ずつ（１ゲーム）転がす。

《結果》

ストライクが出たのは２°～15°の範囲で計45回、特に５°～10°に多く、ポケットもありそうだ。

【実験②】

　ストライク数の多い５°～15°に絞って、さらに20回ずつ（２ゲーム）転がす。

《結果》

実験①との結果を合わせた５°～15°の３ゲーム平均ストライク数は、最多が８°の7.3回、次いで７°の7.0回、９°と10°の各5.7回だった。

【実験③】

より詳しいデータを得るため、範囲を６°～10°に絞り、さらに70回ずつ（７ゲーム）転がす。

《結果》

10ゲーム（100回）平均の角度別ストライク数は、８°が8.0回、７°が7.6回、9°が6.9回、10°が5.1回、６°が4.0回だった。

《結論》

ストライクの出やすい「最高のポケット」は１ピンと３ピンの間、５ピンを中心に８°近くにある。

《２》なぜストライクが出るのか？

角度８°の所ではなぜストライクになりやすいのか。真正面の１ピン（０°）ではどうしてストライクは出ないのか。ボウリング名人は「ドミノ倒しが起きる」とも言っていた。どのようにドミノ倒しが起きるのか、８°ではドミノ倒しがたくさん起きるのではないか。
	1ピンも3ピンも倒れる向きが7ピン、10ピン方向へ

【実験①】

ハイスピードカメラ（１秒間に30枚撮影）で、８°と０°の時のピンの倒れ方を調べる。

《結果と考察》

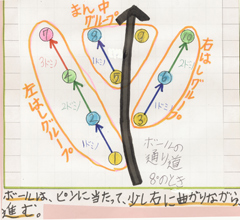
８°の場合、ドミノ倒しは３グループで起きてストライクが取れることが分かった。グループは１ピン→２ピン→４ピン→７ピンと倒れる「左端」グループ、３ピン→６ピン→10ピンと倒れる「右端」グループ、５ピン→８ピンの「真ん中」グループだ。９ピンは１ピンに当たったボールによって倒され、ストライクが取れる仕組みだ。これに対し、０°の場合は、１ピンによって５ピン、８ピン、９ピンの「真ん中」グループでしかドミノ倒しが起きていない。

【実験②】

　１ピンと３ピンの間にボールが入る角度15°では、左端・真ん中・右端の３つのドミノグループができないのか。ハイスピードカメラで撮影する。

《結果と考察》

15°でも３つのドミノグループはできたが、ドミノ倒しが２、３回続く「２ドミノ」や「３ドミノ」がなかったことが８°の場合と大きく違う。ボールの当たった１ピン、３ピンの倒れる向きが、ドミノ倒しを連続させるピンからずれているのだ。

《結論》

ストライクが出るためには①３つのドミノグループと②ドミノ倒しが２、３回連続することの２つの条件が必要で、ボールの角度８°の時が一番条件にあてはまる。

《３》「ポケット」は他にもあるのか？

【実験①】

１ピンと２ピンの間にボールが入ってもストライクが取れた。右８°のポケットだけでなく、ここにもスポットがあるのか。左６°～10°の範囲でボールを１°ずつ10ゲーム（100回）転がす。

《結果》

角度別の平均ストライク数は左８°の時が8.2回で最多、次いで左７°の7.0回、左９°の6.0回だった。

《考察》

左８°も「ポケット」だが、僕と弟が取ったストライクは、１ピンから左右へ離れていくボールのコースだった。左右８°は５ピンに向かっていくコースなので、それとは違う。

【実験②】

右８°の角度線を左に１cmずつ、４ピンまで10㎝平行移動させた10本の線を描き、この10本の線に沿ってボールを10ゲーム（10回）ずつ転がす。

《結果》

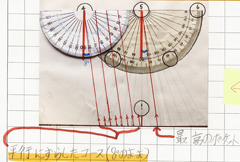ストライクが出たのは第１線と第５線、第６線の各１回だけだった。平行移動では新たな「ポケット」は探せない。

【実験③】

ストライクにつながる「３ドミノ」の起きそうなコースを検討した結果、左右17°の角度線を１ピンから左右に4.5㎝平行移動させたコースがよさそうだと考えた。１ピンから左4.5㎝、右4.5㎝の線にボールを10ゲーム（10回）ずつ転がす。

《結果》

平均ストライク数は、左右4.5㎝ともに5.0回だった。

《考察》

最高の「ポケット」（８°）の平均ストライク数は8.0～8.2回で、その前後でも4.0～5.4回なので、17°の5.0回は「ポケット」とまではいかなくとも、ストライクが出やすいポケットだとは言えそうだ。

【実験④】

ハイスピードカメラで、角度17°の左4.5㎝へボールを転がした時の映像を撮影する。

《結果》

ピンの倒れ方を見ると、やはり３つのドミノグループで、２、３回のドミノが起きていた。

《結論》

①左右17°の角度線を、それぞれ平行移動させた１ピンから右へ4.5㎝、左へ4.5㎝にも「ポケット」はある。
②どの「ポケット」でも、３つのドミノグループで２、３回のドミノ倒しが起きるのでストライクになる。

《４》ボールの速さや重さは、ストライクに関係があるのか？

【実験①】

ボールが速くなると、ストライクは出やすくなるか。実験装置の傾斜レールの角度を変えて、速いボール、遅いボールを転がす。１、３ピンねらいの右８°でそれぞれ10ゲーム（100回）行う。

《結果》

速いボールの平均ストライク数は7.2回、遅いボールは2.9回。《１》の実験③での８°のデータ（ふつうの速さのボール）では8.0回だったので、ボールが遅くなると明らかにストライク数は減るが、速ければ増えるわけではないようだ。

《考察》

結果に納得がいかないので、実験データを詳しく調べた。倒れずに残ったピンの本数を比べたら、遅いボールで10ピンが残ったのは62本と、ふつうのボールの約３倍、速いボールの約10倍と多かった。これは、ドミノの「右端」グループで３ピンから６ピンまでに倒れる勢いが小さく、６ピン→10ピンまでのドミノが起きにくかったからだ。速いボールでは、残った本数が10ピンが６本と少なかったが９ピンが23本と、ふつう・遅いボールの約２倍と多かった。速いボールは「２ドミノ」で10ピンを倒す勢いがあったが、ボール自体が曲がらず進むことが多いので、９ピンが残りやすかったと考えられる。

《結論》

ボールには「２ドミノ」が起きるくらいの勢いは必要だが、それ以上速くなると、勢いが強すぎて「理想のドミノ倒し」ができなくなる。

【実験②】

ボールが重いほど、ストライクはでやすくなるか。ふつう・軽い・激軽いのボールでのストライク数を調べる。右８°で、各10ゲーム（100回）行う。

《結果》

重さ別平均ストライク数は軽いボールが8.4回、激軽いは０回、ふつうボールは8.0回（《１》の実験データから）だった。

《考察》

倒れずに残ったピンは、激軽いでは７～10ピンが50本以上もあった。いずれも一番奥の４列目のピンであることから、ピンを倒す勢いが小さく、４列目までドミノが起きなかったと考えられる。

《結論》

ボールには、「理想のドミノ倒し」が起きる程度の速度・重さは必要だ。しかし、それ以上速くても重くても、ストライク数には関係がない。

研究を終えて

　ボウリング場での疑問を実験で確かめて、いろいろな発見ができたことに満足です。でも頭で分かっていても、実際にやるのは難しいことです。もっと練習をして、いつかストライク名人のおじさんと一緒にプレーしたいです。