研究の動機

　「最短経路」という題で、身の回りのさまざまな自然科学的な「経路」を研究してきた。一昨年は石けん膜を使い、家々を結ぶ最短経路や47都道府県の県庁所在地をすべて結ぶときの最短経路を求めた。昨年は、「迷路の最短経路を探し出す」という「変形菌」に着目して研究し、「変形菌は最短経路を示さない」という自分なりの結論に至った。また、ハチの巣や巻き蔓（つる）の最短経路についても研究した。さらに２年間を通して「シュタイナー問題」を解くことにも力を入れてきた。
　これまでは主に平面的なものについての研究だったので、今回は立体における最短経路＝３次元になるための面の面積＝として「シャボン玉はなぜ球になるのか」について研究する。

研究の目的：シャボン玉が、ただ一つの球になることを示す

《１》シャボン玉はなぜ球になるのか

　シャボン玉は石けん膜でできている。石けん膜は〝面積最小〟になろうとする性質をもつので、空気中のような３次元空間では球になる。『ユークリッド空間内の周期的極小曲面について』（庄田敏宏、数理解析研究所講究録〈1460巻：P53-71、2005年〉）によると、「水中の脂質や界面活性剤などの膜は……極小曲面によって形作られる」とあるので、この小論でも面積最小である面を「極小曲面」と呼ぶことにする。※この「極小曲面」は、閉じた曲面の場合には、特に「平均曲率一定曲面」と呼ぶ。

《２》極小曲面のいろいろ

（1）これまでの研究の見直し

　石けん膜を使った最短経路の研究では、２枚のプラスチック平行板の間に釘をさし、これを石けん液中に入れて引き上げると、釘の間に張った石けん膜がすべての釘を結ぶ最短経路を示すことを実験、および数学的に証明した。
　例えば、平面の三角形（内角がどれも120°未満）の場合、各頂点を結んだ３本の線は１点（フェルマー点）で互いに120°の角度で交わり、その線が最短経路となる。上記研究の平行板の場合は高さがあるので、３本の釘を頂点とした石けん膜がフェルマー点の位置で互いに120°の角度で交わる。そのときの膜も最短経路を示し、面積最小の「極小曲面」といえる。これまで石けん膜を用いて行ってきた最短経路の研究は、いずれも極小曲面を応用したものだった。

（２）多面体における極小曲面

【実験】いろいろな多面体に石けん膜を張り観察する。

《方法》

ポリビニルアルコール（PVA）入り洗たくのりを追加し、膜をより強くした自作のシャボン液（606ml）を使用した。針金で組み立てた正四面体、立方体、正八面体で試した。

《結果》

フェルマー点は正四面体の内部に１つ、立方体に４つ、正八面体には５つできた。

《考察》

石けん膜の面積は各多面体の面に張るよりも、内部に張る方が小さくなる。このことは極小曲面になろうとする石けん膜の性質から、面におけるシュタイナー問題が関係しているといえる。そのために、四角形におけるシュタイナー問題を数学的に証明する。

《証明》

任意の四角形ABCDで、辺AB、辺CDをそれぞれ１辺とする２つの正三角形を描き、各頂点をT₁、T₂とする。四角形ABCDの内部に任意の点P、Qを置くとき、点P₁、P₂がそれぞれフェルマー点だとすると、次の式が成り立つ。

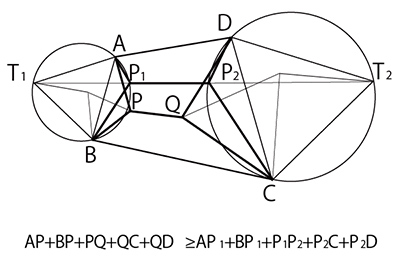
（３）極小曲面は一意的であるか

　結論から言うと非である。針金で作った「本型」「耳当て型」をシャボン液中に入れて、引き上げた。石けん膜（極小曲面）は本型では２通り、耳当て型では３通りできた。引き上げ方の違いによるものだが、いずれも面積は最小だ。同様なことは、釘が４本以上の平行板でも起きていた。上下平行な２つの輪（円）の間にできた石けん膜は、腰がくびれたような形。「カテナリー」という曲線を回転させてできた図形だ。円の間の距離を変えると、形も変化する。

《３》条件付き位相幾何学的考察

（１）本型と耳当て型の共通点

　ともに「折れて覆い被さっている」形だ。ユークリッド幾何学ではなく位相幾何学の考え方でとらえてみる。単純に考えるとすべて円として考えることになるので、条件付けを行う。３点の位置関係を維持して考察すると「中華パン型」の形となる。

（２）球の条件付き位相幾何学的考察

　位相幾何学の世界では、球はどのように変形しても球だ。球でないものとしてあるのは「穴のあいた図形」、それは「トーラス」と呼ばれるドーナッツ型の図形だ。トーラスには２つ穴、３つ穴のものがあるが、今回は１つ穴トーラスについて考える。

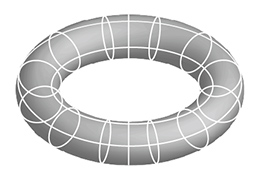
《４》シャボン・トーラスの製作

（１）枠による製作

　位相幾何学で球と区別されるのは「トーラス」と分かったが、シャボン玉が球であることの一意性を証明するためにも、「トーラスのシャボン玉」（シャボン・トーラス）が存在しないことを示さなければならない。
　針金でいろいろな形の枠（いびつな枠、円の中に小さな円のある枠など）を作ったが、石けん膜が面積最小になろうとする性質をもつため、すべて球になってしまう。シャボン・トーラスの製作は不可能だ。

（２）シャボン・トーラスの意図的製作

　シャボン液をつけた枠を、風になびかせるように大きく円を描くように動かすと、細長い筒状のシャボン玉が輪になったシャボン・トーラスができた。

《５》シャボン玉から見たシャボン・トーラス

　球とトーラスの表面積、体積について考察するため、
◆球の半径r₁、球の表面積S₁、体積V₁とする。
◆トーラスの断面円の半径r₂、断面円の中心とトーラス中心との距離t、表面積S₂、体積V₂とする。
　その結果、球の表面積はS₁＝４πr₁²、体積はV₁＝4/3πr₁³となる。
　トーラスの表面積は「パップス＝ギュルダンの定理（第一定理）」を用いると、（回転体の表面積）＝（回転させたい図形の円周の長さ）×（重心が移動した長さ）なので、S₂＝４π²r²tとなる。
　トーラスの体積は「パップス＝ギュルダンの定理（第二定理）」を用いると、（回転体の体積）＝（回転させたい図形の面積）×（重心が移動した長さ）なので、V₂＝²π²r₂²tとなる。
　ここで球とトーラスの表面積、体積がそれぞれ等しい場合について、r₁＝１として計算すると、r₂＝2/3、t＝3/2πとなる。
　ここで2/3＞3/2πなので、「トーラスの断面円の半径（r₂）」は「断面円の中心とトーラス中心との距離（t）」よりも大きく、トーラスの断面円の中にトーラスの中心が存在することになる。前記《４》の（１）でシャボン・トーラスが製作できなかったことに説明がつく。もし可能だとすれば、それはトーラスにおける「平均曲率一定曲面」のようなものだ。

《６》シャボン・トーラスの利用

　シャボン玉の球とトーラスを、人間が居住する実用性の面から比較した。地球上や宇宙空間では、トーラスでは部屋の数や仕切り、居住空間などの点でトーラスの方が優れているようだ。

結論

　シャボン玉には球ではない「トーラス」という形があることを発見した。「トーラス」は実用的で、今後の社会の発展を効率化するために極めて重要なものだと分かった。