市ではゴミの分別収集が行われている。「ゴミ袋の中身が見えないようにするには、ゴミ袋を何枚重ねればよいのか」。学校から照度計を借りて、光の透過量を調べてみた。

《予想１》

１枚のビニールの光の透過率をt（０＜t＜１）と表すと、n枚重ねたときには元の倍の光が透過する。
市指定の燃えるゴミ専用袋のビニール（緑色）１枚では約50％の光が透過した。２枚重ねると「半分の半分」つまり＝25％になるに違いない。３枚重ねるとそのまた半分の＝12.5％、４枚なら＝6.25%と、だんだん中身が見えにくくなるはずだ。

【実験１】

直射日光の当たる場所で、緑色のビニールを１枚ずつ10枚まで重ね、それぞれ透過した光の量を照度計で読み取る。ビニールをピンク（プラスチックゴミ専用）、黄色（有害ゴミ専用）に変えて、同様にデータを取る。

《結果》

①	予測値は、nが大きくなるにつれて実測値からずれる。
②	ずれ方は、実測値＞予測値だ。
③	ビニールは同じ色でも１枚あたりの透過率が異なったが、それでも①②は起きた。

《考察》

測定誤差ならば、予測値よりも小さな実測値も混ざるはず。予測値倍が正しいならば、緑色のビニールを10枚重ねたときは

となるから、透過量は約0.1%と計算できる。これはほとんど光が透過しないことを表す。しかし買ってきた袋は折りたたまれて10枚以上重なっていても、透けて見える。「予測値倍」は誤っているのではないか。

【再実験】

使用した照度計はアナログメーターの針が常にフラフラと動いている。実験精度を上げるため、デジタル照度計のキットを買い、自分で組み立てた。このデジタル照度計を使い再度、緑色のビニールを１枚から10枚まで重ねたとき（これを１セットとする）のそれぞれの光の透過量を1ルクス（lux）単位で、計20セット測定した。

《結果》

《結論》

光の透過率t（０＜t＜１）のビニールをn枚重ねたときは、「元の倍よりもたくさんの光」が透過する。

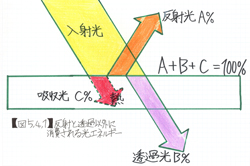
「光の反射」を思いついた。光がビニールに当たると一部は透過し、一部は反射する。２枚のビニールを透過した光というのは実は１枚目、２枚目を反射なしで透過した光のほかに、２枚目で反射して１枚目で再び反射して２枚目を透過する光、さらにこれが２枚目で再び反射して１枚目でまた反射して２枚目を透過する光…などを合わせた光の総和だ。

　 １枚の光の透過率がtのビニールを２枚重ねたときの透過光V2は、最初に当てた光をV、１枚目での透過光をtV、反射光を（１－t）V＝uVとすると、

ビニールを３枚重ねたとき（n＝３）を考える。

２枚目を通過した光をV2とすると、３枚目を透過した光の総和W1、および１枚目に内側からあたる光の総和X1は、図１から、


ここでX1によって２枚目から出てくる光の総和をY1とすると、図２から、

Y1をもとに３枚目から出てくる光の総和W2は、図３から、

　 と表せる。同様に
と続く。

３枚目を透過した光の総和V3は


これまでをまとめると、
となり、n枚のときの光の透過量は、
　と表せる。…【千晶理論】

n=４、n=５、n=６のときの計算値と実験値を比べたら、ほとんど一致した。しかしn=３では約２％理論値のほうが大きい。nが大きくなるほど、ずれも大きくなる。
そこでアインシュタインの「宇宙項」にならい、独自の「Chiaki項」を考えた。「Chiaki項」はビニールの厚みを表す量d（㎜）、硬さを表す量h、温度を表す量c（℃）に関係して決まる量だ。実際にゴミ袋よりも硬く、厚みのあるカラーファイルで光の透過実験をしたら、ファイルのほうが千晶理論とのずれは小さかった（２％以下）。実験後はゴミ袋のほうが暖かかった。「Chiaki項」の関係式などは今回特定できなかったが、この項は完全な千晶理論には必要だ。
【最終千晶理論】ビニール１枚の光の透過率をt（０＜t＜１）とし、n枚重ねたときの光の透過量Vnは、

と表すことができる。