秋山仁特別賞
蚊とり線香のうずまき形と燃え方の関連性について
~蚊とり線香タイマーを目指す~
![]()
山口 咲子
- 千葉県千葉市立緑町中学校 2年
山口 咲子 -
第52回入賞作品
中学校の部
秋山仁特別賞
研究の動機
「うずまき形」に興味をもった。蚊とり線香の燃え方との関連があるのではと思った。そこから、蚊とり線香でタイマーが作れるのではないかと思った。
ステップ1:準備
(1)うずまきの長さを計算する
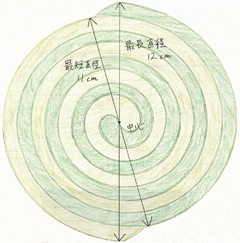 蚊とり線香はうずまき形だ。円ではないので、外側から内側に1周すると、数センチずれてしまう。直線にできないので、面積からおおよその長さを計算する。
蚊とり線香はうずまき形だ。円ではないので、外側から内側に1周すると、数センチずれてしまう。直線にできないので、面積からおおよその長さを計算する。
《方法》
蚊取り線香は2巻き一組なので、一番外側どうしを結んだ最長の直径12㎝(半径6㎝)の大円と、半周分少ない最短直径11㎝(半径5.5㎝)の小円の面積を求める。1巻き分の面積を求めるために各円の面積を2で割り、さらに線香の幅(0.6㎝)で割ることで1巻き分の長さが得られる。この2つの長さを足して2で割ったもの(平均値)が、線香1巻きの計算上の長さだ。
《計算》
大円の線香の長さ:6×6×π÷2÷0.6=94.2㎝、小円の線香の長さ:5.5×5.5×π÷2÷0.6=79.2㎝。計算上の長さは(94.2+79.2)÷2=86.7㎝。
(2) 実測する
蚊とり線香(1巻き)の外側にミシン糸を巻き、その糸の長さを測る。線香の内側に巻くのは大変なので、組になっているもう片方の線香の外側を測る。外側と内側の長さの平均値が、蚊とり線香(幅の中心線)の長さだ。
《結果》
外側88.6㎝、内側66㎝、平均値77.3㎝。
《考察》
外側の実測88.6㎝に(1)の計算結果(86.7㎝)が近かったのは、2つの円の直径を外側で測って計算したからだ。実測と計算との差は、線香の中心部の太さ(幅のふくらみ)にある。計算ではふくらみを考えず、幅すべてを0.6㎝とした。しかし線香はすべてが同じ長さではなく、製品にむらがある。
(3)外側を5㎝間隔で区切る方法
燃え方との関連性から、蚊とり線香を均等に分ける作業は必要だ。最も簡単なのは外側の長さをそろえることだ。
《方法》
ミシン糸に5㎝間隔で印をつける。先端部の斜めカットの終了点から5㎝ごとに区切りを入れ、中心部の太くなる手前でストップする。16パーツができた。
ステップ2:データ収集
(1)実際に燃やして時間を計る
16パーツを漢字表記で一~十六に分ける。先端の斜めカット部分に着火し、A地点から計測を始め、各パーツが燃える時間を計る。蚊とり線香はf社、k社のものを使い、2回ずつ燃焼実験を行う。
《結果》
各パーツの燃える時間は一定ではなく、約20分~22分の間にあった。f社と比べ、k社のものは徐々に燃焼時間が短くなる傾向が見られた。今後の実験はk社のもので行う。
《結論》
蚊とり線香の外側の長さをそろえても、燃える時間は一定にならない。
(2)重さを量る
線香を(1)と同様に5㎝間隔で区切り、16パーツそれぞれの重さを電子てんびんで量る。
《結果》
重さは0.642g~0.826gの間を示した。16パーツの前半よりも後半のものが軽そうだ。パーツ十五、十六はとくに軽い。
《結論》
蚊とり線香は中心に行くほど軽くなる。
ステップ3:発展実験

(1)重さをそろえて燃やす
線香の外側から内側へ、1周ずつ適当な大きさの4個のパーツを切り取る。電子てんびんで量って削りながら、4個すべてを重さ 1.00gにあわせる。それらを同時に着火し、燃焼時間を計った。
《結果》
3回の実験で、燃焼時間は20分50秒~31分5秒の間だった。蚊とり線香の中心部に近いパーツほど、燃焼時間は長くなった。
(2)内側の長さをそろえて燃やす
内側の長さを4㎝にそろえた線香の4パーツを同時着火した。
《結果》
3回の実験で、燃焼時間は24分9秒から31分2秒の間だった。内側の長さをそろえたので、中心に近いパーツほど重い。燃える時間も中心に近いパーツほど長かった。
(3)外側の長さをそろえて燃やす
外側だけを長さ4㎝にそろえたパーツを、同時着火した。
《結果》
中心に近いパーツほど燃える時間は短かった。4本のパーツの重さは、中心に近くなるほど軽い。
【実験結果のまとめ】
| ① | 外側の長さをそろえる→中心に行くに従って軽くなる。 |
| ② | 外側の長さをそろえる→中心に行くに従って燃える時間が短くなる。 |
| ③ | 内側の長さをそろえる→中心に行くに従って燃える時間が長くなる。 |
| ④ | 重さをそろえる→中心に行くに従って燃える時間が長くなる。 |
肝心なのは②と④の性質だ。重さをそろえているのに燃える時間が中心に行くにほど長くなるのは、線香のカーブの角度が燃えるスピードの妨げになっているからだ。しかし、線香の外側の長さをそろえると、今度は中心に行くほど燃える時間が短くなる。さらに外側の長さをそろえてカットすると、中心に行くほど軽くなる。つまり、外側の長さをそろえて燃やした時に中心に行くほど時間が短くなるのは、カーブの角度による燃える時間への影響力よりも、重さによる影響力の方が勝っているからだ。
線香の燃える時間に関連しそうな要素(外側の長さ、内側の長さ、重さ)につい
て調べたが、「これを一定にすれば、燃える時間も一定になる」というものはな
かった。
ステップ4:数学的な分析
蚊とり線香の形について調べる。
(1)面積(S)を表す式を求める
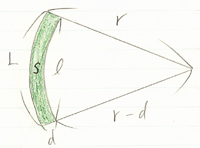 うずまきを円とみなして公式を立てる。大きい扇形の面積から小さい扇形の面積を引く。大きい扇形(半径r、線香の外側の長さL、内側の長さl、幅d)、小さい扇形(半径r-d)
うずまきを円とみなして公式を立てる。大きい扇形の面積から小さい扇形の面積を引く。大きい扇形(半径r、線香の外側の長さL、内側の長さl、幅d)、小さい扇形(半径r-d)
| 大きい扇形の面積: |
| 小さい扇形の面積: |
| 面積(S)= |
これにL=5㎝、r=6㎝、d=0.6㎝を入れると S=2.85㎠。
(2)うずまきの巻数と半径rの関係
うずまきが1周(1巻き)すると、半径はどれだけ小さくなるかを調べる。外側先端を起点(角度0°)に90°、180°、270°地点での1周ごとの半径を測る。線香3巻きの半径の減少はいずれも1次関数(直線)となった。3巻きで直線が一致しないのは製品むらだ。
(3)線香の外側の長さ(L)と内側の長さ(l)の関係
線香の中心に近づくに従い、Lとlの差は大きくなる。Lに対するlの割合が100%の場合は長方形、0%になると扇形だ。
(4)Lまたはlを表す式を求める
Lとlの角度は同じだ。
| つまり | だ。 |
| lについて解けば 、 | 、rを限りなく大きく(線香の外側に行くほど) |
| は0に近づきl=L(つまり長方形)になる。 |
| Lについて解けば | となる。 |
ステップ5:蚊とり線香タイマー
「蚊とり線香タイマー」とは、燃える時間が同じになる「区切り」を見つけることだ。これまでL、l、重さをそれぞれに一定にする「区切り」で実験したが、燃える時間が一定になることはなかった。燃える時間を一定にするには、前記②と④の性質をふまえながら、Lと重さを微調整するしかない。
そこで「重さをそろえること」=「面積をそろえること」と考え、L=5㎝の16
パーツの実験で、燃焼時間が20分台と安定していた「パーツ五」(半径r=5㎝)
の面積(2.82㎠)に一致
| するように、「パーツ一~十六(五は除く)」の各Lを、 | の式から求めた。 |
今後の課題
観察中に、線香が燃えている切断面が常に中心に向いていることに気づいた。外側か内側かが、一方に合わせて燃えていると考えられる。重要なことなので調べてみたい。
審査評[審査員] 秋山 仁
蚊とり線香の「うずまき形」に興味を抱いた彼女は、線香の外側の長さ、内側の長さ、重さに注目し、燃える時間を調べた。その結果、「燃える時間を均等にする線」の入る範囲を特定した。また、実験の中で、重さを一定にし、うずまきのカーブの角度を変えたとき、「カーブが急になると燃え尽きる時間がかかる」ことを指摘した。試行錯誤しながら、科学的にかつ、とても数学的に分析している点は大いに評価できる。
2011年の夏は全国各地で真夏日が続いたが、うだる暑さの中で、蚊とり線香の煙をながめながら科学している彼女の姿を想像し、本作品を大いに楽しませてもらった。





















指導について千葉市立緑町中学校 橋野 未絵
本校では「ひとりいち研究」と称し、毎年全校生徒が科学研究に取り組んでいます。5月頃から授業の中で様々な日用品やおもちゃなどに触れ、身近なところに潜む謎を数多く書き出してからテーマを絞り、研究の進め方も段階的に7月頃まで指導しています。山口さんは数多くのテーマの中から「蚊とり線香の燃え方を利用しタイマーにできないか?」という非常に独創的なテーマを追究することに決めました。テーマ決定後、蚊とり線香の燃え方の規則性など多くの条件について丹念に調査を進め、実験に行き詰まった時も、自分自身で考え抜き根気強く工夫を重ねました。さらに、得られたデータから燃える速さや演習など数学的な視点も加え、領域的研究へと広げました。常日頃から科学へ高い関心をもつ彼女が、熱心に取り組んだ結果、このような賞をいただけたことは大いに励みとなりました。これからも、生徒の好奇心や探求心を育める指導を工夫していきたいと思います。