自然の中で遊ぶのが大好きだ。３年生の時に自然の形を分類する研究を行い、大きな天体や小さな木の実や卵、種（たね）など、自然には「球」という形が数多くあることに気がついた。自然が球を選ぶのには、何か理由があるはずだ。算数を使って形を比べ、実験してみたい。

実験の準備

　球という形の特性を知るために、球と同じ体積の正四面体、直方体、円柱、立方体をシリコン型で作り、比較する。

〈ステップ１〉

元になる球の体積を求める。同じ体積になるように他の立体の展開図を作る。
①買ってきた直径50㎜の球を、透明な立方体の容器に入った水の中に沈め、上がった水位から球の体積を求めた。
立方体の底面積（9.6㎝×9.6㎝）×高さ（0.7㎝）＝64.512㎤
　１㎜以下は正確に測れないことなどから、球の体積を65㎤として考えた。この体積に等しくなるような立体の各部の寸法を計算し求めた。その結果、▽１辺4㎝の立方体▽底面の直径が３㎝のとき、高さ9.2㎝の円柱▽１辺8.2㎝の正四面体▽高さ１㎝のとき、縦・横8㎝の直方体が得られ、それぞれの展開図を作った。

〈ステップ２〉

展開図を塩ビ板にはって、立体を組み立て、石こうを入れて原型を作った。

〈ステップ３〉

石こう原型を粘土に埋め、そこにシリコンを流す。シリコンが固まったら、石こう原型をはずしてシリコン型を作った。合わせ型は反対側も作った。

〈ステップ４〉

シリコン型にポリエステル樹脂を流し、硬化するため炉に入れ、5種類のプラスチック立体を作った。

【実験１】氷を使った温度の保ちやすさの実験

　冬眠中の動物やネコはどうして体を丸くするのか、卵はどうして球の形が多いのか。温度の保ちやすさに関係があるのではないか。

《目的》

氷でそれぞれの立体を作り、溶けやすさ（氷の温度０℃を保ちやすいか）を比較する。

《方法》

シリコン型に水を入れて凍らせ、同じ体積、同じ重さの球、立方体、円柱、正四面体、直方体を作る。それらをネットに入れて吊るし、同じ温度、湿度の空間でどのように、どの順番で溶けていくのか観察し、記録する。条件をそろえるために、重い立体は熱した包丁をあてて溶かし、すべての立体の氷が58gになるようにした。気温は26～27℃。

《結果》

温度を保ちやすい立体の順番（溶けきるまでの時間）は①球（178分）②立方体（169分）③正四面体（150分）④円柱（130分）⑤直方体（60分）だった。

《分かったこと》

予想通り球が最後まで残った。驚いたのは、最初に溶けた直方体と球とは約２時間も差があったこと。２番目に溶けた円柱とも約１時間の差が出た。各立体の氷から溶けた水の重さは、スタートしたときの58gにならずに、少なくなった。蒸発したものと考えられる。「冷たさを保つ」ということは、「温かさを保つ」ということだ。

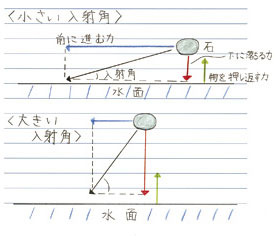
【実験２】　傾斜による動きやすさの実験

　なぜ種や果実は球形のものが多いのか。少しの傾斜も利用して、「子孫をできるだけ遠くに転がし、残したい」ということなのか。

《目的》

傾きのある場所に立体を置き、転がりやすさを比較する。球が動きやすい立体であることを確かめる。

《方法》

摩擦の少ない板（長さ90㎝、幅45㎝）の上にプラスチックの立体（5種類）を置く。板を傾け、立体が動き出したときの角度を記録する。これを10回行い、平均の角度を求める。円柱と直方体は、横に置いたときと縦に（立てて）置いたときについても調べる。

《結果》

動き始めた角度が小さい順に並べると、①球・円柱（横）が１°、②円柱（縦）が12.8°、③直方体（縦）が14.5°、④立方体が16.4°、⑤正四面体が19.6°、⑥直方体（横）が21.6°だった。

《分かったこと》

球と円柱（横）は、実は１°以下で動き始めた。他の立体とは明らかな差だ。種の多くが球形になっている理由が分かったような気がする。球と円柱（横）を同時にスタートさせると、円柱の方が球よりも先にゴールした。動きを見ると、円柱は1つの方向にしか行かなかったが、球はあちらこちらに動きながらゴールに着くので遅くなるのではないか。これが種だったら、あちらこちらに動ける球の形の方が子孫を残しやすい。種が同じところに止まってしまうのは、植物にとっては悪い形だと思う。球と円柱については、芝生など、自然に近い斜面でさらに試してみたい。

【実験３】ホースを使った通りやすさの実験

　どうして卵は球形が多いのだろう。産みやすいのだろうか。立方体や正四面体のように角があったら、痛いかもしれない。通りやすさと関係があるのではないか。

《目的》

どのような形が通りやすいか調べる。

《方法》

直径10㎝、長さ１ｍの透明なじゃばらホースを、垂直に立てたワイヤーネットに針金で固定する。ホースにはカーブをつけ、上からプラスチックの立体（５種類）を入れて、どこまで中を通ってきたかを記録する。立体の到達した区域ごとに、遠い方から近い方に４～１までの点数をつけ、それぞれ10回の合計点で比較する。

《結果》

ホースの中を通りやすい順に①球：40点②立方体：34点③正四面体：22点④円柱：20点⑤直方体：10点だった。

《分かったこと》

球は圧倒的にホースから出てくるのが早かった。正四面体や円柱はカーブでスタックした。球は細い管を通るのに有利な形だ。卵のほとんどが球形なのもよく分かった。

【実験４】脱水機を使ったこわれやすさの実験

　卵が球形なのは「通りやすさ」だけでなく、「こわれにくさ」にも関係するのではないか。もしもこわれやすかったら、中の赤ちゃん（子孫）が死んでしまうからだ。

《目的》

球がこわれにくいことを、他の立体と比較し、確かめる。

《方法》

シリコン型を使って軟らかいロウ、硬いロウの球、立方体、円柱、正四面体、直方体を作る。それらを一緒に厚手のビニール袋に入れて、しっかりと口を結ぶ。その袋ごと脱水機に入れ、1200回転／分で40秒ずつの回転を計100回（計4000秒）行い、立体のダメージを観察する。40秒ずつの回転にしたのは、それ以上だと遠心力が働いてしまうからだ。10回ごとに写真を撮り、記録する。

《結果》

角が多いほど、ロウが軟らかい方ほどダメージは大きく、終了時にはこなごなになった立体もある。ダメージが少ないのは①球②円柱③立方体④正四面体⑤直方体の順だった。

球の特徴

　球は明らかに他の立体と違うことが分かった。球の特徴を、同じ体積65㎤の他の立体と比較した。
（１）表面積：小さい順に①球：78.5㎠②立方体：100.3㎠③円柱：100.7㎠④四面体：116.4㎠⑤直方体：162.2㎠。
（２）中心（投影図の中心）から１番大きな面までの最短距離：長い順に①球：2.5㎝②立方体：２㎝③円柱：1.5㎝④正四面体：1.49㎝⑤直方体：0.5㎝。
（３）中心から１番大きな面までの最長・最短距離の差：小さい順に①球：０㎝②立方体：0.82㎝③正四面体：2.98㎝④円柱：3.34㎝⑤直方体：3.53㎝。
（４）辺の数：少ない順に①球：０本②円柱：２本③正四面体：６本④直方体、立方体：12本。
（５）面の数：少ない順に①球：球面１②円柱：平面２・曲面１③正四面体：平面４④直方体、立方体：平面６。
（６）角の数：少ない順に①球：０個②円柱：２個③正四面体：４個④直方体、立方体：８個。
（７）投影図の最大長：小さい順に①球：５㎝②立方体：6.93㎝③正四面体：8.2㎝④円柱：9.67㎝⑤直方体：11.43㎝。
（８）接地面積：小さい順に ①球：点 ②円柱（横）：線 ③円柱（縦、底面）：7.07㎠ ④直方体（縦）：8.06㎠ ⑤立方体：16.16㎝ ⑥正四面体：29.2㎠⑦直方体：64.96㎠。

《分かったこと》

実験１:氷の溶けにくさとの関係
･表面積が小さいと空気にふれる面積も小さく、それだけ気温の影響を受けにくくなり、溶けにくくなる。球は5立体のなかで最も表面積が小さいので、溶けにくかった。
･球は５立体のなかで中心から一番大きな面までの長さが最も長く、それだけ気温の影響を受けるのも遅くなった。

実験２:傾きによる動きやすさとの関係
･接地している面積が小さいと、それだけ傾斜面で動きやすくなる。球は平面がひとつもなく、接地しているのも点のみなので動きやすい。

実験３:管の通りやすさとの関係
･立体の中心から表面までの長さの長いところと短いところに差がある、バランスの悪い形はひっかかりやすい。球は長いところと短いところの差が全くなく、通りやすかった。
･立体の一番長いところが長い立体ほどひっかかりやすい。球は５立体中で一番長いところが最も短く、通りやすかった。
･角（頂点）が鋭くなっている立体ほどひっかかりやすいが、球には角（頂点）が一点もないので通りやすかった。

実験４:衝撃によるこわれにくさとの関係
･角（頂点）や辺があると、そこがぶつかってこわれてくるが、球にはそれが一点もないのでこわれにくかった。
･立体の中心から一番長いところと一番短いところに差がある立体は、細長かったり薄かったりしてバランスが悪く、こわれやすいが、球は差が全くなくこわれにくかった。

感想

　実験の条件をそろえるのが大変だった。氷は膨張し、プラスチックは収縮するのは、予想していなかった。そのため計算では合っているのに、なかなか同じ重さ、体積にならず、時間がかかってしまった。結果をみて、本当に球はたくさんいいところのある素敵な形だと分かり、ますます好きになった。算数と自然の形がつながっていることも分かり、面白かった。