研究の動機

　家で飼育しているイシガメとクサガメに赤ちゃんが生まれた。とても小さいが、成体と同じようにきれいな模様の甲羅をしていた。よく観察するとカメの背中の甲羅は、さまざまな種類の図形が集まってできている。甲羅の外形（輪郭）は楕円形で、厚み方向に湾曲した曲面を甲板（こうばん）がすき間なく埋めている。カメの背中に次のような疑問が生まれ、調べてみたいと思った。

①

甲羅を構成している甲板は何角形なのか。

②

各甲板は正多角形と比べ、どれだけ歪（いびつ）なのか。

③

年齢によって甲板の形はどのように変化するか。

④

年輪以外でカメの甲羅から年齢を推定することが可能か。

　また、図形の集まりである甲羅について、生物学的解析だけでなく、数学的解析（楕円近似、3色塗り分け、一筆描き）も行い、その違いを調べたいと思った。

生物学的解析 VS 数学的解析

　カメの甲羅は人間でいうと肋骨に当たる部分で、生物学的には、頂甲板、椎甲板、肋甲板（左右1対）、縁甲板（左右1対）、臀甲板（左右1対）に分けられる。しかし、甲羅をサッカーボールのように数学的な図形の集まりと考えると、甲板の種類は関係なく、下の図のように3つの部分で考えることができる。例えば甲板の数を生物学的に見ると、頂甲板1枚、椎甲板5枚、肋甲板左右4枚ずつ、縁甲板左右11枚ずつ、臀甲板左右1枚ずつとなる。数学的に見ると、城3枚、内堀11枚、外堀25枚となる。カメの甲羅の解析には、生物学的に考えるのと数学的に考えるのと、どちらが適しているのか、興味を持った。

研究の内容

　カメの甲羅の不思議を明らかにするため、イシガメとクサガメの甲羅の写真を撮って線で型取りし、甲板の頂点数と角度、面積率を詳しく調べて①〜④の疑問について検討することにした。

調査の対象としたカメ

　家ではイシガメ（10匹）、クサガメ（22匹）を飼育している。そのうち2019年9月に生まれたイシガメ（マーキュリー）と2020年5月に生まれたクサガメ（つくし）、それ以前から飼育しているイシガメ（S、T、E）とクサガメ（ひめ、国）の合わせて7匹を実験の対象に選び、生物学的解析と数学的解析の両方で、身体的特徴を調べることにした。

解析の準備

　カメの甲羅をできるだけ真上から数十枚写真撮影し、甲羅の中心線から左右の長さがほぼ同じ写真を選んだ。
　選んだ写真をプリンターで印刷し、白紙を重ねて光にかざして甲羅の甲板を線で型取りした。甲板の境が分かりにくい時は、実際のカメを観察して線を描き加えた。これを線図形図と呼ぶことにした。次に、型取りした紙を複数枚コピーし、線と線が交差したところに点を付けた。これを点図形図と呼ぶことにした。点の数と、線の数を数えた。
　線図形図の甲板の線が作る角度を分度器で測定した。頂点の数はその甲板が何角形かを表しているが、甲板が歪な場合があるため、合計の角度からも何角形かを調べることにした。正n角形の内角の合計角Aは式で表せる。

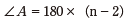
　正n角形の1つの角の角度Bは、次のように求める。

　例えば正三角形ならば内角の合計は180°、1つの内角は60°になる。正四角形ならば内角の合計360°、1つの内角は90°、正五角形ならば内角の合計540°、1つの内角は108°になる。正多角形の場合、内角の大きさで何角形か判断できるが、カメの甲板は歪で分度器で測っても角度にばらつきがある。1つの内角が75°以下なら三角形、75°より大きく99°以下なら四角形、99°より大きく114°以下なら五角形というように、ある程度の範囲を持たせて多角形を判定することにした。

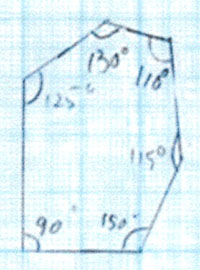
　カメの甲板の多角形が歪になるのは、カメの種類や性別、年齢などが原因かもしれない。そのため、正多角形からのずれを数値で表すことを考えた。正多角形からのずれはさまざまな基準から数値化できるが、この研究では内角の角度からずれを数値化することにした。そのばらつきを「内角の最大値から最小値を引いた値」と、「標準偏差の値」で考えることにした。
　標準偏差というのは、まず右上の図のような六角形の場合、次の数式で分散s2を求める。

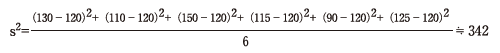
　さらに分散s2を使って、標準偏差を次のように求める。

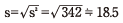
　この方法で、7匹の甲板すべてのずれを数値化した。

数学的解析の方法

　数学的解析では、下の図のように甲羅の外周を楕円で近似した。

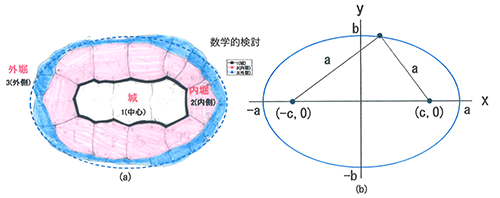
　頂甲板部分は少し凹んでいるため、隣の縁甲板を考慮して甲羅全体の輪郭を決定し、aを求めた。近似楕円と実際のカメの外周の差も考慮する。近似楕円の線に沿って線図形図の紙を切り、実際のカメの外周に合わなかった部分の面積を評価することにした。
　また、3色塗り分けにも挑戦した。隣り合った甲板を同じ色で塗らない場合、すべてを3色以内で塗り分けられるかというものだ。塗り分けられない場合、その部分の特徴を考えた。塗り分けられない甲板の合計数と年齢とが、関係していないかを調べてみた。
　さらに、一筆描きでカメの線図形を描くことにも挑戦し、描けない部分について、その特徴を考えた。通れた線の個数が、年齢と関係していないかも調べてみた。

まとめ

　さまざまな解析の結果、以下のことがわかった。

①

甲羅を構成している甲板の中央部分は六角形、その周りは五角形、一番外側は四角形が多かった。

②

甲板は正多角形ではなく、標準偏差で20〜30°のばらつきがあった。

③

正多角形から角度のばらつきは年齢により増加すると予想したが、イシガメ、クサガメともに、その傾向を確認できなかった。

④

甲板の頂点の角度、面積率、3色塗り分け、一筆描きなどでは年齢と相関が見られなかった。唯一、年齢との相関が見られたのは、数学的解析で甲羅全体を楕円近似した際の長軸と短軸の長さの比だ。しかしそれも、年齢を決定するほど、きれいな傾向は確認できなかった。

⑤

線図形、点図形で解析する場合、対象がカメという生物であっても、生物学的解析より数学的解析のほうが統計的なまとまりがあり、適していることがわかった。

　今後は、甲羅を世界地図のように3次元から2次元に変換することに挑戦したい。