理科の授業で、だ液の働きの実験をした時、60℃の湯に25℃の水を加えて40℃の湯を作ったが60＋25＝85ではない。その他考えると、温度のたし算について不思議なことが起こっているように思えた。そこで、温度について、たし算できるのはどんな場合か、たし算できないときは、どんな計算をしたら良いかを調べたいと思った。

□ml，△℃の湯と、○ml，▽℃の水を混ぜて□ml＋○ml，？℃のぬるま湯ができると考えたとき、？を□△○▽の式で予言したいと思った。

実験１　湯と水の量が等しいとき

①湯をナベで大量にわかした。②メスシリンダーで100mlの水をビーカーに測りとった。③温度計で水の温度を測った。④湯をメスシリンダーで100mlビーカーに測りとった。⑤湯の温度を変えて
②と混ぜた。⑥湯と水を温度計で5回ゆっくりかき混ぜて温度を測った。⑦湯の温度・水の温度・できたぬるま湯の温度を棒グラフに表した。

結果

できたぬるま湯の温度は湯と水の平均になった。

湯と水の量が違うとき

湯の体積と温度を変えて実験した。結果できたぬるま湯と水との温度差をA、ぬるま湯と湯との温度差をBとすると、□：○＝A：Bであることを発見した。ぬるま湯の温度＝（▽×○＋△×□）／（□＋○）（千晶理論１）を導けた。

検証実験

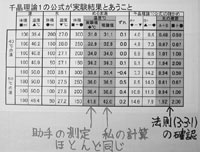
1）（父に助手になってもらった）①湯と水の量を助手が測り私に伝えた。②助手は湯と水を混ぜてぬるま湯の温度を記録した。③私は千晶理論１を使ってぬるま湯の温度を計算した。④結果を照らし合わせた（表１）。
2）氷と水（湯）を混ぜたとき、
3）0℃の水と湯を混ぜたときで調べた。

表1

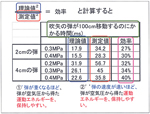
千晶理論１は検証されたが、氷と水（湯）を混ぜた場合には当てはまらなかった。同じ0℃でも氷は水よりも冷やそうとするパワーが強いようだ。さらに、熱い湯の冷め方を詳しく調べて、「湯の温度の下がる速さは、その瞬間の湯の温度と周りの温度の差に比例する」（千晶理論２）ことが予想できた。