秋山仁特別賞
街の中の数学Ⅱ
―エスカレーターとベクトル―
柴垣 休卯
- 東京都小平市立小平第六中学校 2年
柴垣 休卯 -
第58回入賞作品
中学校の部
秋山仁特別賞
研究の動機
あるエスカレーターに「歩くな」の注意書きがあった。日本ではエスカレーターの片側で立ち止まる人、もう片方を歩く人がいるのが一般的だ。そこで昨年は、エスカレーターを歩かずに両側に人がいる場合と片側を人が歩いている場合とで、どちらが効率よいのか研究した(「街の中の数学―エスカレーターと渋滞理論―」)。そこでは観察とコンピューターモデル、初歩的な数理解析によって「エスカレーターは、片側を人が歩く乗り方よりも、両側に人が立ち止まっている方が効率的だ」との結論を得た。しかし、エスカレーターの段数や利用する人の数などの「初期値」の違いで、結果が変わることに気づいた。より完全な形で昨年のテーマに迫りたいと思い、さらに研究する。
I.昨年の研究から
昨年の研究では『エスカレーターの乗り方のパターンA(片側が止まり、片側は歩く)、パターンB(両側が止まる)、ρ(流量)、T(乗った人全員を運び終わる時間)とすると、次の関係が成り立つ。
ρA < ρB、TA > TB ......定理3
これにより「AよりもBの方が、短時間で多くの人を運べる」(定理4)』とした。
II.流量ベクトル-モデル
《1》数学を用いたアプローチ
(1)昨年の課題を解決するためのモデル
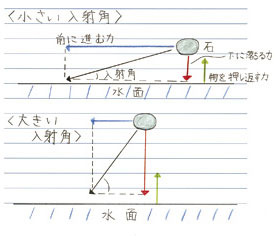
昨年はエスカレーターに乗る人を点としてモデル化したため、「乗る人の数」「エスカレーターの段数」という初期値の変化に対応できず、「歩く人の速さ」も理論に組み込めなかった。そこで今回は、人の流れをベクトルとして表す。人の動く方向がベクトルの矢印の方向、歩く速さが矢印の長さだ。そのベクトルをここでは「流量ベクトル」、そのモデルを「流量ベクトル-モデル」と呼ぶ。
(2)モデルから導かれる定理
流量ベクトル-モデルから、直ちに〈定理1:流量ベクトルの本数は、その時点のエスカレーターにいる人数と等しい〉が導かれる(図①)。
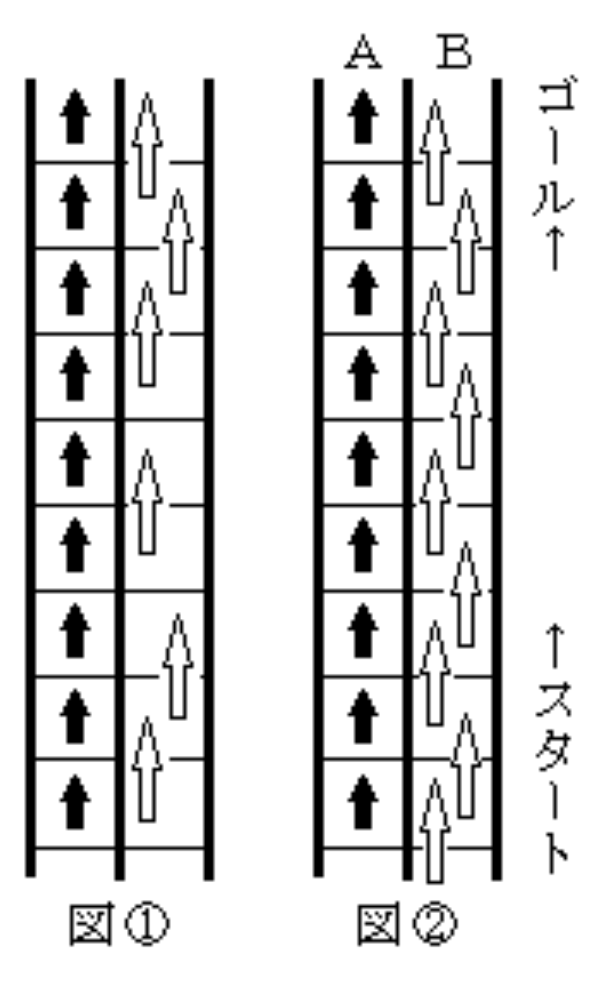
(3)流量ベクトル-モデルから読み取る情報
図②で、エスカレーターの左側(A)で止まっている人の速さを1、右側(B)を歩いている人の速さを2とするとエスカレーターのB側で運べる人数は、A側の2倍となる。よって〈定理2:エスカレーターの左側・右側に同人数が乗っているとき、歩きの速い人が乗った側がより多くの人を運べて効率がよい〉が導かれる。
《2》流量ベクトルを用いた数理解析による展開
エスカレーターの長さ(段数)をL、人の速さをv、運べる人数をPとおくと、
vA < vB、LA = LB さらに定理2から
PA < PBとなる。
しかしこれは、ある時点のエスカレーターのスタート~ゴール間のことで、人の運動は考えに入れていない。
(1)展開
上の例で、エスカレーターのB側を歩く人数(PB)は、全体の人数(K)の1/n(n≠0)とすると、
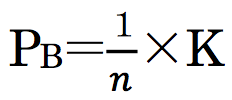となり、さらに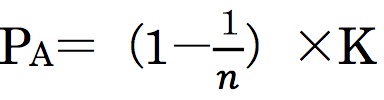
定理2から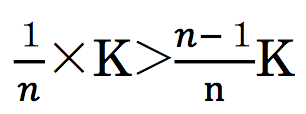
となるので
K > (n-1)KここでK > 0により1 > n-1、さらに
n < 2となる。この条件下でPA < PBが成り立つ。
(2)考察
上記の展開から、次の定理が導かれる。〈定理3:図②においてB側を歩く人数を(全体の1/n)、A、Bが運べる人数をPA、PBとおくと、n < 2ならばPA < PBとなる。〉
これはn < 2が成立条件であり、n > 2の場合は〈定理4:図②においてB側を歩く人数を(全体の1/n)、A、Bが運べる人数をPA、PBとおくと、n > 2ならばPA > PBとなる。〉が導かれる。これは、B側よりもA側を利用する人が多ければ、A側はB側よりも効率よく人を運べるということだ。
《3》理論の一般化
《2》ではエスカレーター右側(B)のどの段にも必ず人がいる状態で論を展開してきた。実際には、人がいない段もある。そのような場合を考えて一般化する。
(1)人数Pに関する展開(1)
人が立っていない(ベクトルの始点がない)段の総和をℓ、すべての段に人がいるときに運べる人数をp、速さをvとおくと、実際に運べる人数Pは、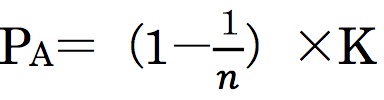で求められる。
ここでℓ < L、v ≠ 0とすると、次の定理を得る。〈定理5:図①において、B側を歩く人が全体の1/n、B側のベクトルの始点がない段の総和をℓとおくと、nが増加するとℓも増加する。〉
(2)人数Pに関する展開(2)
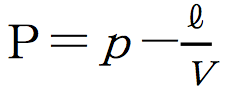において、ℓが取る最小値をℓmin、最大値をℓmaxとおくと、
ℓ< Lで ℓmin = 1、ℓmax = L - 1 となり、
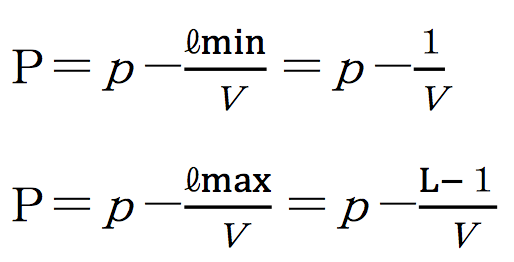
さらに ℓmin < ℓmax であるから
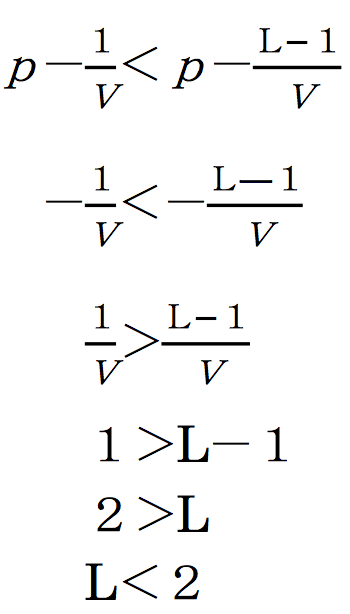
したがって、L < 2 ならば ℓmin < ℓmax となる(定理 6)。
(3)一般化への準備
VA=1、VB=2でLA=LBとするエスカレーターがあると、Aは止まっている人の側、Bは歩いている人の側となる。B側でだれも立っていない段の総和をℓとすると、
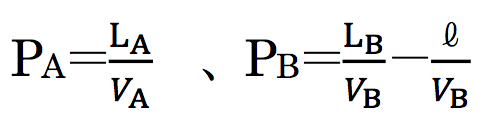
よって、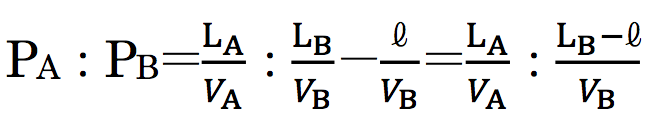
VA=1、VB=2であるから
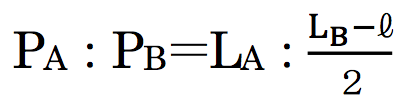となる。
さらにLA=LBなのでLA=LB=Lとおくと、
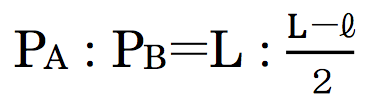
さらにPA:PB=2L:L-ℓ、よってPA>PBとなる。
このことから、エスカレーターの両側に人が止まる乗り方(I型)と片側は歩いて片側は止まる乗り方(II型)とでは、VA=1、VB=2のときは、エスカレーターにとってI型の方が効率がよい。
(4)一般化
エスカレーターで、立ち止まっている人がいる側をA、歩いている人のいる側をBとする。エスカレーターが動く速度をVA=α、B側の人が歩く速度をβとすると、B側の人が動く速度はVB=α+β(α>0、β>0でVA < VB)。B側で流量ベクトルの始点がない段の総和をℓ、エスカレーターの長さをLとすると、A側、B側で運べる人数PA、PBの関係は、
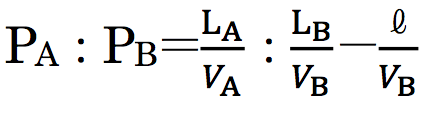
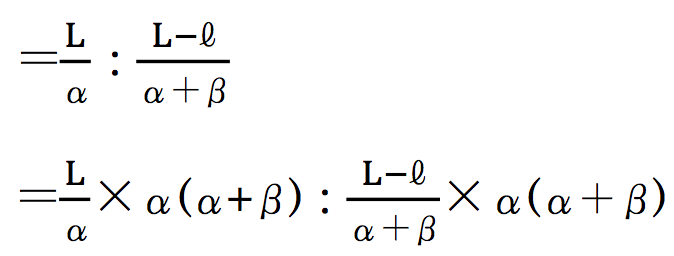
=L(α+β):α(L-ℓ)と表され、
L >ℓ、α+β > αであることから、
L(α+β) > α(L-ℓ)、さらにPA > PBとなる。
《4》結論
3段以上のエスカレーターでは、利用者の半分より少ない人数が片側を歩いている場合より、各段の両側に人が立ち止まっている場合の方が多くの人を運べて効率がよい。......定理7
審査評[審査員] 秋山 仁
この研究は、昨年の研究の続きです。エスカレーターの乗り方を「両方とも止まる(パターンI)」と「片方が歩き、片方が止まる(パターンII)」の2つに分け、どちらが効率的(すなわち、多くの人を運べる)かについて分析しています。昨年の結果をより精度を高めるため、今回はエスカレーターの段数や利用者の人数を考慮に入れて分析しています。また、人の動きをベクトルで表現し、問題を数理モデル化している点は評価に値します。結論は、3段以上のエスカレーターで、パターンIIで利用者の半分が歩く側を利用すると仮定すると、パターンIの方がパターンIIより効率的であることを導いています。エレベーターが団子状態になることを数理的に解明する理論(待ち行列の理論)は広く研究されていますが、エスカレーターについてはあまり知られていないので新規性もあると思います。
指導について柴垣 茂之
昨年、佳作をいただいた「街の中の数学ーエスカレーターと渋滞理論ー」では、片側を歩行できるように空けた方がいいのか、それとも空けずに並んだ方がいいのか、その効率を数学的に考察するものでした。そこでは空けずに並んだ方が、30%ほど効率が良いと結論づけましたが、人の混み具合という変数によって結論が変わってしまう点が依然として課題として残っていました。今回、研究テーマを継続するか新しいテーマに挑戦するか悩んでいる様子でしたが、たまたまベクトルの考え方を学び、そこでヒラメキがあったようです。ベクトルを人の動きに応用することで課題解決の糸口をつかむに至ったとは本人の弁。この場は指導についてのコメントという事ですが、恥ずかしながら私自身が数学に強いとはとても言えないものでして、特に指導や助言をすることもなく、資料のプリントアウトなど雑務等の後方支援に徹しました。