昨年の夏休みに「The独楽～“直観でバランスを取ること”について科学的な根拠を探求し、任意平面図形を回すための一考察～」に取り組んだ。コマの軸を作図で求める方法を推論し（「Ka」理論）、作図の原理を使って軸決定装置を考案したりした。そしてこれを中学２年までの数学で証明した。今年は平面を立体に拡張してみたいと思い、調べるうちに、偶然にも数学の定理を独力で発見してしまった。この定理を、三平方の定理ならぬ「四平方の定理」と名付けた。

（1）発見に至るまで

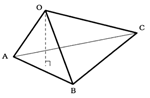
立体の基本図形として、立方体の一部を切り取ってできる合同な３枚の直角三角形と１枚の正三角形からなる三角錐を考えた。頂点Oを通るコマの軸は、底面△ABCに垂直になる。直方体から切り取った三角錐では、頂点から底面への垂線が軸にはならない。「Ka」理論から△ABCの重心が重要で、△ABCの面積について考える必要が生じた。

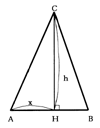
（2）OA、OB、OCの長さが与えられたとき、△ABCの面積を求める。

①OA、OB、OCを与える。
②三平方の定理から

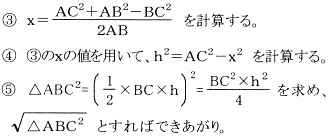
（3）四平方の定理に向けて

（4）新発見「河合の定理」

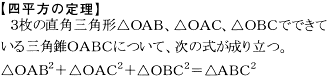
《証明》

三角錐△ＡＢＣの△ＯＡＢ、△ＯＡＣ、△ＯＢＣは直角三角形。ＯＡ＝ａ、ＯＢ＝ｂ、ＯＣ＝ｃと表す。 三平方の定理により△ＡＢＣの各辺が計算できるので、ＡＢ＝ｋ、ＢＣ＝ｌ、ＣＡ＝ｍとすると、次の式が成り立つ。

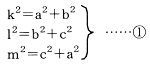
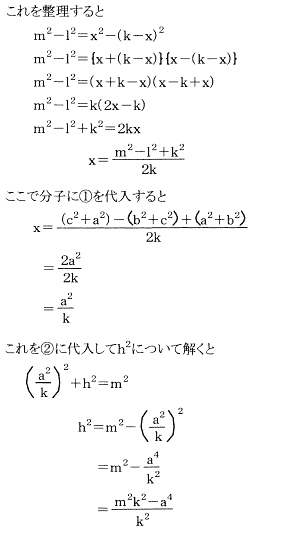
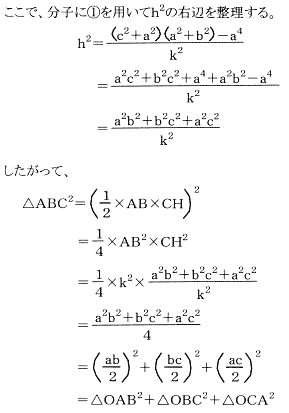
（証明終わり）

（5）四平方定理の意義について

三平方の定理は、３辺に接する３枚の正方形の面積についての美しい関係だ。辺の２乗は正方形の面積を表すから、定理を図形的に解釈したり、式の意味を味わうことができる。ところが「四平方の定理」では「三角形の面積の２乗」の意味がまったく不明だ。図形的に何を意味するのか。四平方の定理もとても美しい優美な定理だが、先行研究を調べても、すでに発見されていることは確認できなかった。数学者にとって取るに足りない程度の定理なのだろうか。

おわりに

新定理の発見とその証明の成功を体験した。自然科学を創造することがこんなに面白いものだったとは。数学や理科を学ぶ目標が見えてきた夏の体験だ。