自分が現在研究している「フィボナッチ数列の周期的予想」の研究を進めるにつれて、度々現れる「黄金比」が自然界によく現れていることを知り、その理由を解明しようと考えたからである。

方法

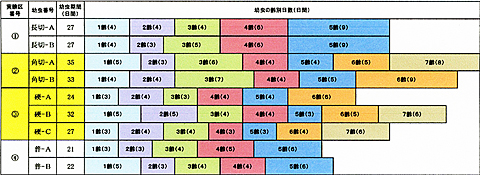
自分とデータ協力者8人の左手の親指・人差し指・中指・薬指・小指の指先から第一関節までの長さ（末節骨）・第一関節から第二関節までの長さ（中節骨）・第二関節から第三関節までの長さ（α）を測定して記録した。 利き手は「ペンを持つ手」と決めた。
実際の長さ①→末節骨：（末節骨＋中節骨）、実際の長さ②→（末節骨＋中節骨）：（末節骨＋中節骨＋α） （データ1）。

分析

データより、指の関節どうしの長さの比率を計算し、それがどれだけ黄金比に近いかをパーセンテージで表したものを「近似率」とした。近似率は黄金比との差分を黄金比で割り、それを１から引いたものとした。

9人の比率（①と②）で近似率が95％を超える黄金比に近い指の比になっていたのは、小指（9カ所）、中指（9カ所）、人差し指（5カ所）、親指（4カ所）、薬指（3カ所）だった。右利きと左利きを同じ割合に直したとき、親指を除いて左利きの方が黄金比に近いカ所数が多かった。左利きは左手に、右利きは右手に黄金比が割合的に多く現れてくるのは利便性に関係があるからだと考えた。普段使わない小指や薬指に黄金比が出現していることから、利き手でしか使わない動作を観察するつもりである。
　また、末節骨とαが等しいのは、指を折り曲げる際に便利であるからだと推測された。しかし、それでは末節骨と中節骨の長さが黄金比であることの証明はできない。さらに、「何かをつまみあげる動作」では関節にあたる部分は7カ所あるが、実際にはだいたい5カ所の関節が動いていた。5/7カ所の関節が動作している場合、指の長さに関係があるとは考えられない。ゆえに、指の長さの比は黄金比にはならないと考えている。

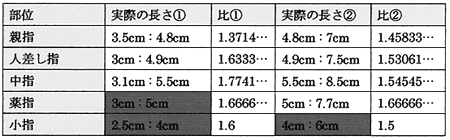
データ１