秋山仁特別賞
You are the Champion!
~大相撲巴戦に関する先行研究の理論拡張と、ジャンケン必勝法の発見~
![]()
河合 千晶
- 三重県鈴鹿市立神戸中学校 3年
河合 千晶 -
第50回入賞作品
中学校の部
秋山仁特別賞
大相撲の巴戦には「公平な対戦ではない」との違和感があった。秋山仁先生の解説によると、わずか7%だが、最初に対戦しなかった力士に不利な状況があるという。しかしそれは3力士の互いの勝率を1/2と仮定するなど、理想化された状態での数学的考察だ。力士の連戦の疲れや対戦待機中の精神的な重圧などが勝率に影響しないのか、いろいろな疑問がわいた。そこで平成21年夏場所の全316対戦をビデオにとり、対戦時間や決まり手、「時間です」までの駆け引きなどを分析した。さらに日本相撲協会や相撲部屋、中・高体連相撲部門、三重大学教育学部などに手紙や直接訪問するなどして、検証のためのアイディアを相談した。本研究では、そのままでは科学の土俵に乗せにくい課題を整理し、数学的理論を拡張した。
大相撲の巴戦:力士A・B・Cが同率のとき、
| ① | 抽選で最初の対戦A対B(待機C)を決める。 |
| ② | A対Bの勝者がAのとき、次にA対Cを行う。 |
| ③ | A対CでAが勝ったら、力士Aが優勝。 |
| ④ | ③でCが勝ったら、C対Bを行う。 |
| ⑤ | 以下、同様に対戦を進め、2勝の力士が出たら、その力士を優勝者とする。 |
平成21年夏場所の全316対戦の分析:所要時間は全対戦の90%が26秒以下で、平均時間は11~12秒だった。3~4秒が最も多く37対戦、4~5秒が32対戦、5~6秒が25対戦、2~3秒が22対戦と、一瞬で決まることが多かった。
先行研究をネット検索していたら、秋山仁先生の巴戦についての解説「秋山仁のこんなところにも数学が(70)~大相撲の巴戦は不利な結果に」があった。
【力士A・B・Cの互いの勝率を1/2と仮定し、最初にA対Bを行う場合、Aの優勝する確率をp(A)、Bの優勝する確率をp(B)、Cの優勝する確率をp(C)と表すと、
p(A)=p(B)=5/14、p(C)=4/14となる。】
第1戦で待機していた力士Cが優勝する確率は、
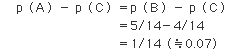
となり、7%ほど、A・Bよりも優勝する確率が低くなる。
A対BでAの勝つ確率=p、B対CでBの勝つ確率=q、C対AでCの勝つ確率=rのとき、(1)力士Aの勝つ確率p(A)をp、q、rの式で表せないか。(2)Cがどれくらい強いと、損をしないか(巴戦が公平になるか)。
相撲の巴戦の勝敗を、ジャンケンの勝敗に対応させるモデル実験を試みた。3人1組となってジャンケンし、誰かが連勝するまで続ける。家族や友人などの協力で1万回のジャンケンのデータを得た。
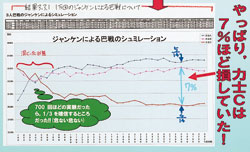
その結果、3283回の巴戦のシミュレーションができた。700回を超えたあたりからp(C)はp(A)、p(B)よりも小さくなった。2300回を超えたあたりからp(A)=p(B)=5/14、p(C)=4/14に近づいてきた。さらに、Cは対戦3、6、9、12、…回目に優勝すること。A、Bは対戦2、4、5、7、8、10、11、…回目に優勝することも分かった。これは・最初の対戦結果で、その後の対戦順序が決まる。・3人の力士が何回目の対戦で優勝するかは、自動的に決まる――ということだ。
「千晶多項式」
(1)Aが第1対戦で勝ち、優勝する場合。優勝確率をChiaki(A、○)とすると
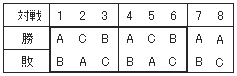
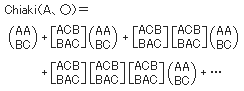
(2)Aが第1対戦で負け、優勝する場合。優勝確率をChiaki(A、×)とすると

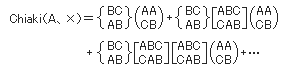
(3)Aが優勝する確率 Chiaki(A)は、
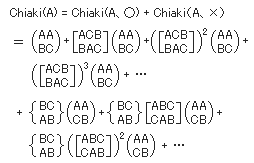
A対BでAの勝つ確率=p、B対CでBの勝つ確率=q、C対AでCの勝つ確率=rのとき、
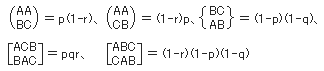
と表せる。上式に代入すると、

◇力士はどれくらい強いと、巴戦は公平になるか
第1対戦のA、Bは強さが等しいと考えるとp=1/2、さらに、q=1-rとすると
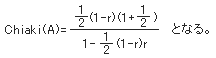
公平な巴戦はChiaki(A)=1/3であるから、
![]()
◇どれくらいCが強いと公平になるのか
![]()
となり、8%ほど強いと公平になることが分かる。
1万回のジャンケンでは、勝者、敗者、あいこを入れて合計29842個(グー:10159回、チョキ:9425回、パー:10258回)の手のパターンが記録できた。あいこで連続したのは4921回、連続して同じ手が出たのは合計3563個あった。グーとパーのあいこでは、次に連続して同じ手が出やすいが、チョキが続くかどうかは何とも言えない。
《結論》
①パーをなるべくたくさん出す。
②あいこのときは、あいこの手よりも強い手を出す。
③チョキであいこになったら、運に任せる(①に従うと有利だ)。
審査評[審査員] 秋山 仁
本研究は、大相撲の優勝決定戦の一つである巴戦の不公平さに端を発した作品である。
3人の力士A、B、Cによる巴戦のとき、最初に対戦する力士をA、Bとすると、彼ら2人が勝つ確率はどちらも5/14に対し、控え力士Cは4/14で約7%不利である。この事実を確率を計算して求めるだけでなく、ジャンケンを何千回も行い、実際に確かめているのは特筆すべきだ。また、その関連として、ジャンケン必勝法を導いていることも有り難い。今度チャンスがあったら彼女の戦略に従うつもりだ。
さらに、巴戦で3人の力士の力量(勝つ確率)が異なる場合についての一般式を導いているのは驚きだ。その他にも、確率に関する多くの結果を導いている。たとえば、丁半バクチで、丁、半どちらに賭けても5分5分のはずが、昔は丁に賭ける方が有利であると誤解されていた理由も明解に説明されている。
ひとつの不思議から出発して、次々に関連する問題を見つけそれらを解決するチャレンジ精神に敬礼!
























指導について鈴鹿市立神戸中学校 藤井智子
6月頃から自由研究の題材として「海水はなぜしょっぱいのか」、「ピーマンの空洞の気体を調べるにはどうしたらいいか」などと質問を受けていました。私自身が1年前まで大学で研究していたため、身近にないような機械を使った実験をすぐに思い起こしてしまい、あまり参考にならなかったようです。7月の半ば頃、新たに「疲れの度合いや疲れからの回復を調べるためにはどうしたら良いか」と質問を受けました。私は持久走の前後に測定する心拍数を調べる方法と、血中酸素濃度を測定する方法を提案しました。
それから1カ月、彼女は数学の教員である両親や高校生の兄と相談しながら、難しい計算の方に力を注いだようです。彼女がどこまで計算の方法や意味を理解しているかわかりませんが、気になったことをノートに書き留めたり、徹底的に調べたり、精力的に周囲の人に教わろうとするその旺盛な好奇心は、私にとって大変刺激的でした。