研究の動機

　時代劇に、サイコロを使った丁半賭博の場面が出てくることがある。時として眼光鋭い侍がそのサイコロを奪い刀で真っ二つにすると、中から鉛の玉が出てくることがある。「イカサマ」がバレて大騒ぎになる。
　そこで疑問に思ったのは、サイコロにおもりを入れることで、本当に出てくる目を操作できるのか、ということだ。この研究では、サイコロにどんな細工をすれば「IKASAMA」が可能になるかを明らかにし、この世の闇に迫っていきたいと考えた。

研究の目的と方法

研究の目的

　研究の目的は、次の3点だ。サイコロに仕組むおもりの位置や重さによって、目の出る割合がどのように変わるのかを明らかにする。目の出る割合が変わる理由を、力学的に考察する。研究の結果をもとに、自分たちの考える究極の「IKASAMAサイコロ」を作製する。

自作のサイコロを定義する

　研究の前にいくつかの予備実験を行い、「共通実践事項」を決定した。まず、自作するサイコロの材料は特定メーカーの同じ紙粘土とし、形は正六面体、一辺の長さは2cm（±2mm）とする。仕組むおもりはすべて直径5mm、鉛球（密度11.35g/㎤、質量0.96g）、鉄球（密度7.87g/㎤、質量0.51g）、アルミニウム球（密度2.70g/㎤、質量0.18g）を使った。

サイコロの振り方と回数

　サイコロの振り方は、両手の中で3回以上サイコロを振り、高さ10cmから机上に向かってサイコロを転がす。サイコロを振る回数は180回とした。

データ分析の方法

　データ分析は、そのサイコロで「狙った目が出る割合」を調べることがまずひとつ。普通のサイコロを同じように振れば、ある目が出る割合は1/6で16.7%になるはずだ。イカサマで特定の目が出る割合が、16.7%より大きくなるのかを確かめる。
　実験ではサイコロを180回振ることにしているが、当然そこにはばらつきが生まれる。そのばらつきが偶然起こり得るものなのか、偶然ではあり得ないものなのか、検定によって確かめる必要がある。今回は「カイ2乗検定」を行い、統計学的に確認することにした。

カイ2乗検定の方法

❶ サイコロを180回振って、1〜6の目が出る回数をそれぞれ調べる。
❷ ❶の回数と期待値（180回÷6=30回）との差をそれぞれの目で求める。
❸ ❷で求めた差を基に、カイ2乗値を求める。

❹ ❸で求めたカイ2乗値を棄却値11.07（自由度5、α=5％）と比較する。
❺ カイ2乗値＞棄却値ならば「ばらつきは偶然起こっているものではなく」、カイ2乗値＜棄却値ならば「ばらつきは偶然起こり得る範囲内である」と、結論づけた。

研究の実際

何も仕組まないサイコロの性質の確認

　「IKASAMA」を調べる前に、何も仕組まないサイコロでは、本当に目の出方に偏りがないのかを確認することにした。市販のプラスチックのサイコロ（一辺の長さ1.5cm、質量3.94g）を180回振り、各目の出る割合を比べると、多少のばらつきはあるが大きな偏りはない。カイ2乗値を求めると5.13で、棄却値11.07より小さく、ばらつきは偶然起こり得る範囲内だった。
　何も仕組まない自作のサイコロでも目の出方を確かめた。自作のサイコロ3個でカイ2乗値を求め、棄却値と比較したところ、3個とも棄却値より小さい値だった。

さまざまなおもりを仕組んだサイコロを振る

　自作のサイコロに鉛、鉄、アルミニウムのおもりを仕組み、目の出方の変化を調べてみた。サイコロはおもりを入れた面を下に止まりやすく、おもりの反対側の目が出やすくなるはずだ。おもりの位置をそれぞれ下の図のように変えながら、ねらった目が出る割合と、カイ2乗値をそれぞれ算出した。

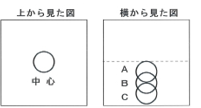
　その結果が、下のグラフだ。

さまざまなおもりを仕組んだサイコロの目の出方

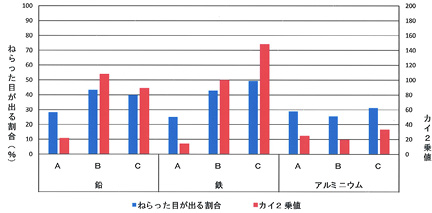
　ねらった目が出る確率は素材では鉛＞鉄＞アルミニウム、おもりの位置ではA＜B＜C、と事前に予想を立てていた。素材は「鉛C」以外ほぼ予想どおりだったが、おもりの位置で予想どおりだったのは鉄だけだ。鉛とアルミニウムではなぜ位置予想が外れたのか、考えてみた。

「慣性モーメント」の比較

　おもりの位置での予想が外れた原因は、サイコロの転がりにくさにあるのではないかと考えた。サイコロの中心からおもりの位置までの距離が長いほうが、短いものより回転しにくくなる。この回転しにくさが「慣性モーメント」で、ねらった目が出にくくなる原因ではないか。この仮説を立証するため、モーターでサイコロを回転させる時に必要な消費電力を比較したり、40度の斜面から地面に向けてサイコロを転がし、地面を転がった距離を比較したりした。すると「鉛B」より「鉛C」のほうが、明らかに転がりにくかった。「アルミニウムA」と「アルミニウムB」でも斜面の実験をしたところ、「アルミニウムB」のほうが転がりにくいという結果だった。
　転がらなければおもりを下に止まりにくいため、目を出すためには転がりやすさも重要だと確かめられた。

重心の位置を確かめる

　おもりの位置や種類で目の出方が異なるのは、それぞれのサイコロの重心の位置が違うためだと考えられる。そこで、「吊り下げ法」で重心の位置を調べることにした。「吊り下げ法」とは物体を異なる2点で糸とつなぎ吊り下げ、それぞれの鉛直線（地面へ糸が指す方向線）の交点を重心とする方法だ。その結果、おもりの質量が大きいほど、そしておもりの位置が下にあるほど、重心は下へ移動し、ねらった目が出しやすくなることがわかった。

重心の位置と転がりにくさの兼ね合い

　ねらった目を出しやすくするためには、「転がりやすさ」と「重心位置」が決め手になることがわかってきた。おもりの数を増やしたり、おもりの入れ方を変えたり（集中型と拡散型を比較、単体型と縦列型を比較など）して確かめたが、いずれもおもりの質量が大きく重心が下にあるほうが目が出やすい。ただ、転がりにくいものは重心が下になっていても効果は薄まった。

究極の「IKASAMAサイコロ」作り

　研究を基に、究極の「IKASAMAサイコロ」を考えた。
　「奇数サイコロ」はサイコロの1つの頂点（角）のすぐ内側に鉛球1個を仕組む。この頂点のおもりのおかげで非常に転がりやすい。頂点に接していない3つの面を奇数（偶数にもできる）にすることで奇数の出現率は85.6%、カイ2乗値は113.3となった。まさに、丁半賭博にうってつけのサイコロだ。
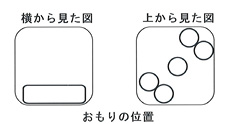
　その他、「九鉛無角目(きゅうえんむかくもく)」は9個の鉛球を底面すぐ上に一段になるよう並べ、サイコロのすべての角を直線的に小さく削ったもの。ねらい目の出現率88.9%、カイ2乗値は678.3。「大福目(だいふくもく)」は1個の鉛球を底面中央すぐ上に仕組み、すべての角を丸くしたもの。ねらい目の出現率96.7%、カイ2乗値は830.4だった。「頂点重点目(ちょうてんじゅうてんもく)」は5個の鉛球を底面に下の図のように並べ、すべての角を丸くしたもの。ねらい目の出現率99.4%、カイ2乗値は888.1だった。